
Конев В.В. Дифференцирование функций
Разность между функцией и её многочленом Тейлора называется -м остатком , или -м остаточным членом ; обозначим этот остаток через :. Если считать, что остаток мал, то его можно отбросить без большой погрешности; при этом получается приближённая формула. Выясним, в каком смысле можно понимать "малость" остатка в формуле Тейлора, чтобы этой приближённой формулой мы могли пользоваться осмысленно. Теорема 6.








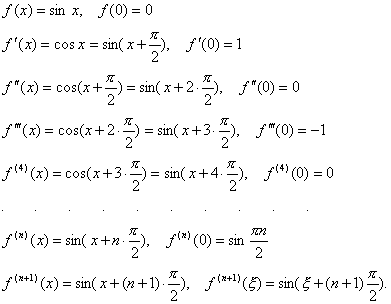

Даем определения производной и дифференциала. Разбираем правила дифференцирования и выводим формулы производных для основных функций. Рассказываем о формуле Тейлора и правиле Лопиталя. Из равенств 11 и 9 следует формула 8.







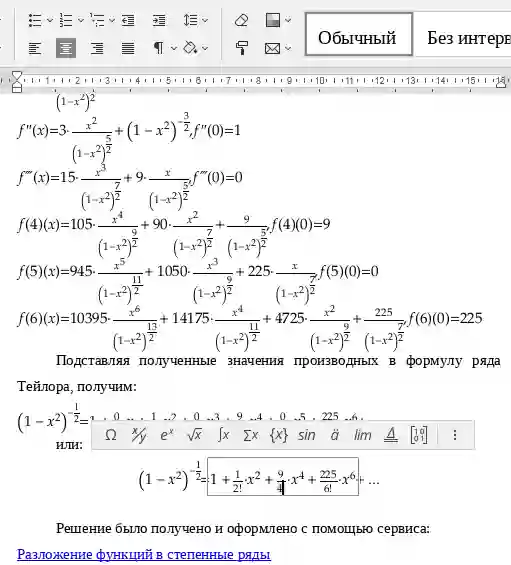
Пусть функция f x определена в некоторой окрестности точки x0 и n раз дифференцируема в точке x0. Они уточняют формулу 1. Теорема 1 Пеано. Пусть функция f x имеет в точке x0 производные до n—го порядка включительно. Теорема 2.




